Tatiana quer ensinar na universidade, motivando os alunos, e contribuir para a pesquisa em Matemática. Em certa medida, já faz tudo isso: está fazendo seu mestrado em Geometria Diferencial e dá aulas num cursinho voluntário para indígenas. “Passar o conhecimento e entender o mundo são coisas que me fazem bem.” Quando criança gostava de brincar com exercícios de Matemática; foi incentivada por professores, mas foi sua mãe quem lhe ensinou a fazer conta de divisão. Se inspira em outras mulheres matemáticas, mas gostaria que houvesse mais. “Frequentemente acham que sou de humanas, porque me interesso por muitas coisas; sou uma pessoa plural.” Toca violão e adora a praia de Itacaré, na Bahia, sua terra natal.

Os números naturais são os primeiros números que nos são apresentados na vida: 0, 1, 2, 3, 4, e assim por diante. Não existe o maior de todos os números naturais, pois todo número natural n possui um sucessor, n+1, que também é um número natural. Além disso, com exceção do número 0, todo número natural é sucessor de algum outro.

Ao se estudar as bases que constituem a Matemática, surge a necessidade de precisar o que exatamente esse “e assim por diante” da primeira frase quer dizer. A maneira mais tradicional de se fazer isso é introduzindo o chamado Princípio da Indução Finita (PIF):

——

Se X é um conjunto satisfazendo:

– 0 pertence a X

e

– para cada n que pertence a X, tem-se que seu sucessor, n+1, também pertence a X,

então X contém todos os números naturais.

——

O PIF pode ser visualizado por meio da seguinte ilustração:

Imagine que você tem uma fileira infinita de dominós, representando os números naturais. Existe um dominó que é o primeiro da fila, mas não existe o último: cada dominó tem um sucessor, que está logo à frente dele.

Nesta ilustração, o PIF corresponde à afirmação:

Se o primeiro dominó for derrubado e cada dominó que cai também derruba o próximo da fila, então todos os dominós serão derrubados.

O que você acha? Faz sentido?

Uma outra maneira de se pensar no conjunto dos números naturais é considerando uma propriedade chamada Princípio da Boa Ordenação (PBO):

——

Se A é um conjunto não vazio de números naturais, então existe algum elemento de A que é o menor de todos os números que pertencem a A.

——

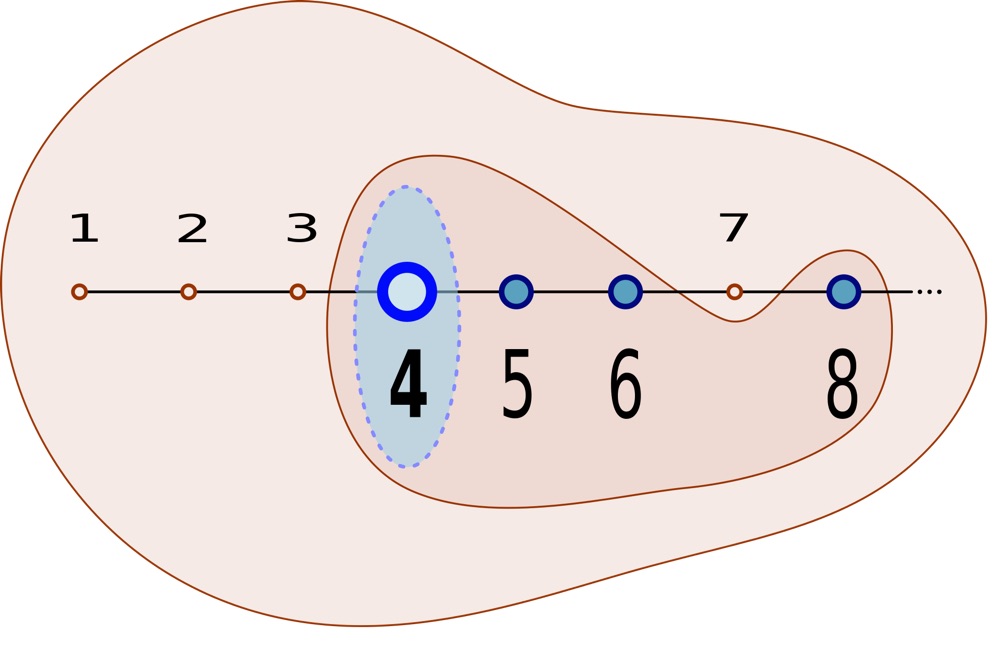
O que você acha dessa afirmação? Faz mais sentido que o PIF? Ou menos?

A grande surpresa aqui é que o PIF e o PBO, apesar de serem afirmações que parecem bem diferentes, na verdade são equivalentes! Qualquer uma dessas duas afirmações pode ser introduzida para explicar como é o conjunto dos números naturais — o “e assim por diante” do começo do texto —, e elas conduzem à mesma descrição.

O PIF e o PBO ilustram muito bem um fenômeno bastante interessante que se observa em várias partes da Matemática: muitas vezes, conceitos matemáticos são desenvolvidos em contextos diferentes e surgem com formulações diversas ao longo da história; mas uma análise posterior mostra que se trata do mesmo conceito. O PBO já era empregado na matemática da Grécia Antiga, ao passo que o PIF veio a ser formulado somente no século XVII. E, em sua essência, ambos descrevem a mesma estrutura no conjunto dos números naturais.