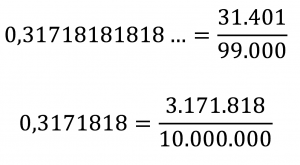Thais sempre quis ser professora — tanto pelo gosto por explicar as coisas para os amigos desde pequena, quanto pela convicção de que ensinar pode mudar a perspectiva das pessoas sobre o mundo e sobre quem elas são. A escolha pela Matemática foi natural: a beleza dos conceitos, independentemente de suas possíveis aplicações; o fato de a Matemática estar presente no mundo e ao mesmo tempo ser uma construção humana; a clareza do pensamento dedutivo; a segurança que ela proporciona; os vários caminhos para se chegar à mesma resposta — tudo isso a fascina. Hoje, após ter concluído a Licenciatura em Matemática e o mestrado em Ensino da Matemática, cursa Pedagogia como segunda graduação. É professora de Matemática no Ensino Básico e não se vê fazendo outra coisa. “Eu acredito que a razão de estarmos no mundo é interagirmos uns com os outros, para que a gente aprenda: ‘eu não sei todas as coisas, eu não sou a verdade, a minha perspectiva é apenas uma dentre todas as perspectivas possíveis’. Acho que essa troca é muito importante.”

O conceito de número racional é simples e sofisticado ao mesmo tempo. Todos somos familiarizados desde cedo com números decimais (por exemplo, para contar dinheiro ou medir nossa altura) e com frações (o exemplo clássico é a divisão de barras de chocolate). Intuitivamente, desenvolvemos a noção de que tanto os números decimais que possuem dígitos depois da vírgula quanto as frações representam quantidades que não são inteiras. Mas o que esses dois objetos têm a ver um com o outro? E o que vem a ser um número racional, afinal?

O conjunto dos números racionais não pode ser facilmente descrito por uma listagem natural de seus elementos em ordem, como ocorre com o conjunto dos números naturais N = {0, 1, 2, 3, …} e o conjunto dos números inteiros Z = {…-3, -2, -1, 0, -1, 2, 3, …}. Isso se deve ao fato de que os números racionais possuem uma ordem que satisfaz uma propriedade muito especial: entre quaisquer dois números racionais distintos, sempre existe um número racional entre eles — basta tomar a média aritmética dos dois números, que também será um número racional. Em particular, se x é um número racional, não se pode determinar qual é o “próximo” número racional na ordem em que eles estão dispostos — simplesmente porque esse “próximo” número não existe! Em outras palavras: não existem dois números racionais consecutivos!

Muitas pessoas, quando apresentadas a essa afirmação, se perguntam: mas o número 0,9999… não é o maior número menor que 1? Então esses dois números seriam racionais consecutivos, certo?

Não é bem assim… Na verdade, temos aqui um fato que é um tanto surpreendente: o número 0,9999… é igual a 1. E o argumento para mostrar isso é relativamente simples: se chamarmos de x o número 0,9999…, podemos multiplicar por 10 cada um dos lados da igualdade e obter 10x = 9,9999… . Agora, subtraindo a primeira igualdade da segunda, chegamos em 9x = 9, ou seja, x = 1.

Isso evidencia algo muito importante: 0,9999… e 1 são duas representações diferentes do mesmo número — assim como 3/4, 15/20 e 0,75 são representações diferentes de um mesmo número!

Podemos, assim, dar uma resposta à nossa pergunta inicial: um número racional é aquele que pode ser escrito em forma de fração (com numerador e denominador inteiros, claro). E esses são exatamente os números que possuem uma representação decimal em que uma mesma sequência finita de dígitos se repete indefinidamente — e, no caso em que essa sequência é apenas o dígito 0, isso equivale a uma representação decimal com uma quantidade finita de dígitos depois da vírgula.