Aline é uma professora de Matemática com aspirações de artista. “Queria fazer Artes Plásticas, mas, no cursinho, percebi que a Matemática era uma espécie de pedra no sapato das pessoas.” Ela não sentia essa dificuldade e isso despertou a curiosidade de compreender esse processo. “Me interessei pela licenciatura, porque queria entender como as pessoas aprendiam.”

Em Matemática, gosta do que é contraintuitivo, “do que se vê, mas não se acredita”. Na sua opinião, para torná-la acessível para os alunos, é preciso lançar mão de exemplos cativantes, de problemas interessantes.  “Aprendi muito num estágio em que assistia a oficinas e tive contato com vários materiais que não são livros-texto.”

Após lecionar por vários anos, Aline hoje trabalha na área de avaliação educacional e atua junto à formação de professores, além de se dedicar à pequena Clara.

A noção de infinito causa assombro e fascínio em diversas épocas do conhecimento. Na Grécia Antiga, por exemplo, o filósofo Zenão de Eleia elaborou o seguinte “paradoxo”: Aquiles decidiu apostar corrida com uma tartaruga. Como ele é mais rápido que a tartaruga, definiu-se que a tartaruga começaria a corrida na frente de Aquiles. Segundo Zenão, Aquiles nunca seria capaz de ultrapassar a tartaruga, pois quando Aquiles chegasse à posição inicial da tartaruga, A, esta se encontraria mais à frente, numa outra posição B. Quando Aquiles chegasse à B, a tartaruga não estaria mais lá, pois teria avançado para uma nova posição C, e assim sucessivamente.

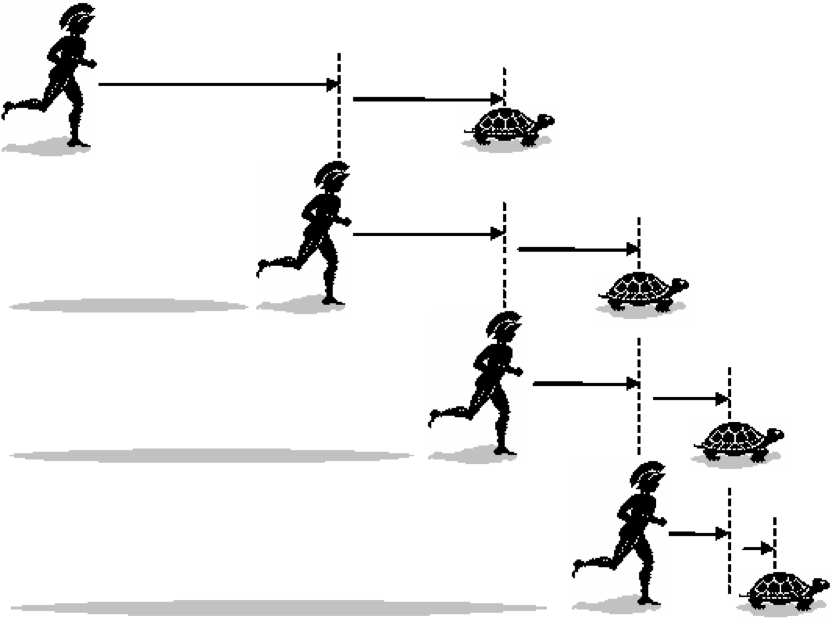
Na prática, sabemos que Aquiles ultrapassará a tartaruga. O que produz essa confusão? A resposta é simples: assumir, implicitamente, que uma soma infinita de números positivos será necessariamente infinita! Imagine que Aquiles corre 1 metro por segundo, enquanto a tartaruga percorre 0,01 metro no mesmo tempo. Suponha, ainda, que a tartaruga comece a corrida 1 metro à frente de Aquiles. Após 1 segundo, Aquiles chegará à posição A. Após 0,01 segundo, Aquiles chegará à B. Após 0,0001 segundo, Aquiles chegará à C, etc. Dessa forma, Aquiles levará 1 + 0,01 + 0,0001 + … segundos para alcançar a tartaruga. Como essa soma corresponde à soma dos termos de uma progressão geométrica (PG) infinita, ela resultará em 1/(1 – 0,01) = 100/99. Isso significa que, transcorridos 100/99 segundos, Aquiles ultrapassará a tartaruga.

O Hotel de Hilbert tem uma infinidade de quartos, um para cada número natural.

Um viajante chega e pede um quarto ao recepcionista. O recepcionista informa ao viajante que o hotel está lotado, mas que dará um jeito de atender a sua solicitação: ele pede ao hóspede do quarto 1 que vá para o quarto 2, ao hóspede do quarto 2 que vá para o quarto 3, e assim por diante. Em outras palavras, ele desloca quem estiver no quarto n para o quarto n+1. Desse modo, todos continuarão alojados e o quarto 1 ficará livre para acomodar o viajante. Horas depois, quando chega ao hotel um ônibus com 30 passageiros, o recepcionista pede que todos aqueles que estiverem no quarto n se dirijam para o quarto n+30 e, em seguida, acolhe todos os recém-chegados.

No fim do expediente, ele recebe uma infinidade de passageiros, tantos quanto o número de quartos do hotel. O recepcionista, antes de ir para casa e descansar após um árduo dia de trabalho, resolve a questão da seguinte maneira: ele transfere quem está no quarto n para o quarto 2n. Assim, consegue acolher todos esses passageiros sem desalojar ninguém!

Esta anedota ilustra o fato de que existem tantos números pares quanto números naturais. E tão surpreendente quanto isso é o fato de existirem infinitos de tamanhos diferentes! Mas esta já é uma outra história…