Monyze Negreiros Silva

Monyze se prepara para fazer sua segunda graduação: seu sonho é estudar Estatística. Queria ser professora desde pequena e não se sentia desafiada na área em que trabalhava. “O que estava esperando acontecer? Decidi fazer cursinho e me preparar para o vestibular.” Diz que gosta muito de estudar — “tudo” — e quer usar a Estatística como ferramenta para explicar fenômenos; se encanta com a perspectiva de fazer novas descobertas. “Gosto de perceber padrões e de relacionar meus conhecimentos para chegar à solução de um desafio. Curto a sensação de estar descobrindo coisas.” Enxerga Matemática até na música de sua viola e na maneira como se formam as filas do metrô.
CURVA GAUSSIANA
No século XVII, ciente de que os instrumentos de medições astronômicas eram imprecisos e de que havia erros de observação, Galileu notou a simetria dos dados coletados e, também, que pequenos erros ocorriam com mais frequência que grandes erros.
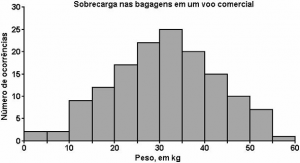
Ocorre que fenômenos de natureza bastante diversa possuem uma distribuição com comportamento deste tipo, que é conhecida como distribuição normal. Veja, por exemplo, a distribuição da sobrecarga de bagagens em voos comerciais.
Já no século XIX, Gauss formulou a Lei de Distribuição Normal como um princípio que rege estes fenômenos. Consideremos a distribuição da altura de uma pessoa adulta da população americana, separadas por gênero.
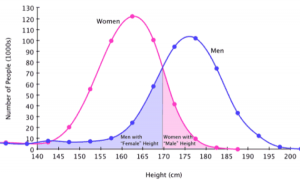
Nos dois casos, temos uma distribuição que forma esta figura em forma de sino. Mais ainda: se, em vez de altura, considerarmos o peso de uma população, a pressão sanguínea, o desempenho dos estudantes numa prova ou tempo numa corrida, a distribuição será similar, formando esse “sino”, que é uma curva gaussiana.
Voltando à figura, quando consideramos a população feminina, o “centro” está perto de 162cm. Isso mostra que essa é a altura feminina mais comum, que mais mulheres têm (chamada moda). Para a população masculina, o centro parece estar perto de 178cm. As amplitudes das curvas (variância) também são ligeiramente diferentes. A equação das curvas gaussianas é dada em termos da média e da variância.
