Marilda é licenciada em Matemática e atua como professora de Ensino Médio e de cursinho pré-vestibular há 30 anos. Incentivada por colegas de trabalho e pela família, decidiu encarar um mestrado profissional em Matemática. “O mestrado me abriu um horizonte diferente e tem me acrescentado muito, tanto na qualidade das minhas aulas quanto no relacionamento com os alunos. O ganho é diversificado.” Para ela, a Matemática é dinâmica, objetiva, sem rodeios e, principalmente, uma ferramenta de escolha, de decisão. Fascinada por sua utilidade prática, procura apresentar exemplos interessantes a seus alunos, mostrando que a Matemática não está só na área de exatas: “Ela, por exemplo, está presente na genética e pode até mesmo influenciar a decisão de um juiz num tribunal”.

Questões envolvendo probabilidade muitas vezes desafiam a intuição. Imagine que uma pessoa fez um teste para detectar uma doença que atinge 1% da população. Segundo o laboratório, há apenas 5% de chance de se obter um falso positivo e apenas 5% de chance de se obter um falso negativo. Qual a probabilidade de a pessoa estar doente sabendo que o teste deu positivo?

Se você fizer o teste e for positivo, certamente vai ficar bem preocupado. Feitas as contas, a resposta parece bem mais encorajadora: cerca de 16%. Surpreendente, não? A confusão que fazemos instintivamente é entre as perguntas: “qual a probabilidade de a pessoa estar doente sabendo que o teste deu positivo” e “qual a probabilidade do teste ser positivo sabendo que a pessoa está doente”. Esta última questão tem resposta 95%. Mas o dado com grande impacto que se costuma negligenciar é o fato de a doença atingir apenas 1% da população.

Queremos saber a probabilidade de um evento ocorrer (no caso, “a pessoa estar doente”) levando em consideração que um outro evento ocorreu (“o teste deu positivo”).

A Regra de Bayes resolve esse tipo de problema. Ela dá a probabilidade de um evento A ocorrer tendo em vista que um evento B ocorreu, P(A∨B), e é definida como a probabilidade de A e B ocorrerem, P(A∧B), dividida pela probabilidade de  ocorrer, P(B). Como P(B∧A) = P(A∧B), segue que P(B)·P(A∨B) = P(A)·P(B∨A). Dividindo a última igualdade por P(B) obtemos:

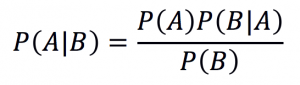
Nos anos 1990, houve uma grande polêmica a respeito de um desafio que ficou conhecido como Problema de Monty Hall. A resposta correta, mas nada intuitiva, dada pela colunista de jornal Marilyn vos Savant, gerou muitas cartas de reclamação, inclusive de matemáticos.

Monty Hall (apresentador do Let’s Make a Deal, programa televisivo exibido nos EUA na década de 70) apresentava 3 portas a um jogador, sabendo que atrás de uma delas havia um carro e que atrás das outras havia bodes. O jogador começava escolhendo uma das portas. Antes de abri-la, o apresentador abria uma das duas outras portas não escolhidas pelo jogador, mostrando um bode dentro dela. Em seguida, ele pergunta ao jogador se este deseja manter a escolha anterior ou mudar para a outra porta. Sabendo que o jogador ganhará o prêmio que está atrás da porta que escolher, pergunta-se: qual escolha lhe dá maior probabilidade de ganhar o carro?