Renata tem a Matemática no sangue. Mãe, pai e tio lecionam a disciplina. Quando criança, seu desejo era ser como eles e “fazer Matemática com letrinhas” — conceito curiosíssimo para uma aluna do Ensino Fundamental. O caminho até a profissão atual — gerente de risco de uma administradora de cartões de crédito — foi repleto de desvios: cursou licenciatura em Matemática e passou uma temporada lecionando numa escola estadual antes de se interessar por Estatística e optar por um emprego no mercado financeiro.  Mas, afinal, o que faz uma gerente de risco? “Busco padrões, segmento clientes e ofereço o produto mais apropriado àquele cliente.” O que desperta a sua paixão pelo trabalho, no entanto, é o desafio diário de solucionar problemas. “A graduação em Matemática desenvolve o raciocínio lógico; é uma formação que capacita o indivíduo para exercer inúmeras profissões.”

Imagine a seguinte situação:

Dois fabricantes de balas de goma vendem pacotes com balas coloridas. Nos pacotes do fabricante A, 20% das balas são roxas; já nos do fabricante B, as balas roxas são 30% do total. Joãozinho abriu um desses pacotes e pegou 8 balas ao acaso, das quais 2 eram roxas. Com base nessa informação, pode-se ter um palpite sobre qual o fabricante do pacote que Joãozinho abriu?

Uma pergunta desse tipo ilustra bem como Probabilidade e Estatística tratam de problemas diferentes: a Probabilidade procura estimar, a partir de certos parâmetros já conhecidos, a chance de certos eventos ocorrerem; já a Estatística analisa eventos que já ocorreram e procura, a partir deles, extrair informações sobre os parâmetros envolvidos. Mas a Probabilidade e a Estatística dialogam bastante, como veremos a seguir.

Vamos chamar de p a proporção de balas roxas nos pacotes de um determinado fabricante; assim, p é um número entre 0 e 1, e 1–p é a proporção de balas de outras cores (não roxas) nos pacotes. Isto significa que, se escolhermos ao acaso uma bala do pacote, a probabilidade de ela ser roxa é p, e de não ser roxa é 1–p. Sendo assim, ao retirarmos 8 balas de um pacote desse fabricante, a teoria da Probabilidade garante que chance de 2 delas serem roxas e as outras 6 não serem roxas é

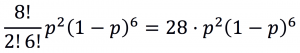
Podemos então substituir p pelos valores informados no enunciado. Para o fabricante A, temos que p = 0,2; nesse caso, se retiramos 8 balas, a chance de que 2 sejam roxas e 6 de outras cores é de aproximadamente 29,36%. Para o fabricante B, temos que p = 0,3 e obtemos uma probabilidade de 29,65%. Como essa é mais alta para o fabricante B, é mais plausível que o pacote aberto por Joãozinho tenha sido do fabricante B!

O que fizemos foi calcular, para cada um dos fabricantes, a probabilidade de que ocorra um evento — sejam retiradas 8 balas de um pacote dele, sendo 2 delas roxas e 6 de outras cores — e escolhemos então como mais provável o fabricante que tem a maior probabilidade de que isso ocorra. Se nos pacotes de balas de um terceiro fabricante C, 40% das balas são roxas, obtemos que a chance de que ocorra esse evento é de 20,90%, de forma que B continua a ser o fabricante mais provável.

Esse problema é um exemplo do que se chama “estimador de máxima verossimilhança”. O objetivo é encontrar, a partir da amostra de eventos considerada, os valores dos parâmetros que maximizam a probabilidade de acontecer precisamente o que foi observado. Esse tipo de ideia tem aplicações em áreas muito diversas (de bancos de investimento a cálculos de seguros), nas quais se deseja otimizar certos modelos estatísticos para que eles representem da forma mais acurada possível a realidade que os dados mostram.