Natural de Osasco, Andressa gosta da brisa do mar, mas se diz cunhense de coração. Acaba de concluir um mestrado profissional em Matemática, sobre os números primos. É professora de Ensino Médio na rede estadual, assim como seus pais, e apaixonada pela profissão. “Sou professora de Matemática, mais do que matemática”, enfatiza. Sente que, ao ensinar um adolescente a raciocinar, não traz benefícios apenas para a Matemática: incentivar os alunos a pensar é fundamental para desenvolver seu espírito crítico e prepará-los para a vida em sociedade. Todas as suas ambições profissionais estão numa sala de aula. “O que me move é que, na sala de aula — onde entrei pela primeira vez aos quatro anos de idade e de onde nunca mais saí — posso mudar um pouquinho o mundo”, justifica. Até seu gosto pessoal dialoga com a profissão: foi o livro Uma professora muito maluquinha, de Ziraldo, que despertou seu gosto pela leitura.

Andressa teve contato com a Conjectura de Goldbach no seu trabalho de mestrado. Esse é um dos mais famosos problemas “em aberto” (ainda sem solução) sobre números inteiros. Ganhou mais notoriedade ainda depois que Andrew Wiles provou o Teorema de Fermat.

Um número primo é um número inteiro, maior que 1, e que não tem divisores exceto ele mesmo e 1. São números primos: 2, 3, 5, 7, 11, 13, 17, 19 etc. O alemão Christian Goldbach, numa carta ao matemático Leonhard Euler, conjecturou que todo inteiro par maior que 2 pode ser escrito como soma de dois números primos.

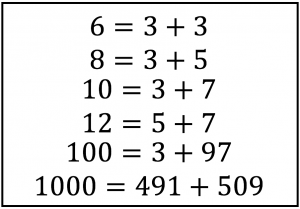
No quadro acima, testamos alguns números pares. Com a ajuda de computadores, já foram checados (pelo menos) todos os números até 4·10¹⁸ e todos os pares testados podem ser escritos como a soma de dois primos. Mas será que é verdade para todos os números pares? Até agora, ninguém provou que sim e nem que não.

Outra questão simples de enunciar e que desafia os matemáticos há séculos é o problema dos “primos gêmeos”. Dois números primos são gêmeos se a diferença entre eles é 2. Por exemplo, os pares (3,5), (5,7), (11,13), (17,19) são pares de primos gêmeos. A pergunta para a qual ninguém sabe a resposta (até agora!) é: existem infinitos pares de primos gêmeos?

Existem infinitos números primos e uma elegante demonstração desse fato foi dada por Euclides cerca de 300 anos antes da nossa era. Mas o problema dos primos gêmeos continua sem solução.

Todo número inteiro pode ser escrito (de forma única) como produto de números primos. O fato de não termos uma maneira “rápida” de decompor um número (grande) em fatores primos é o que garante a segurança da criptografia usada na Internet, pelos bancos etc. A ideia é que demora tanto para um programa “quebrar” um código que passa a ser seguro. Olhe abaixo o quadro com uma notícia do jornal O Estado de São Paulo.