Anne curte cuidar de sua horta e adora cheiro de livro novo. Gosta de Matemática desde criança, quando resolver um problema era tão prazeroso quanto passar de fase num jogo de videogame. “Matemática não se trata apenas de fórmulas decoradas; a Matemática é divertida.” Participou de Olimpíadas de Matemática e, influenciada por seu irmão, também matemático, fez graduação, doutorado e três pós-doutorados (ufa!) antes de se tornar professora doutora no Departamento de Matemática da Unicamp. Nascida em Ribeirão Preto (SP), foi graças à Matemática que morou em Brasília, Campinas, Chicago (EUA) e Rio de Janeiro e conheceu inúmeros países, além do marido. “Ser professora e pesquisadora em Matemática é uma profissão muito legal.”

O conceito de limite é um divisor de águas na vida de estudantes do primeiro ano de faculdade em todas as carreiras da área de exatas. Ele é fundamental para o Cálculo Diferencial — as definições de derivada e integral de uma função dependem deste conceito — e é a partir dele que a Matemática ganha uma nova perspectiva aos olhos dos jovens, por estudar o comportamento de objetos matemáticos como funções ou sequências de números, no lugar de estudar instâncias destes objetos.

A noção de limite está associada à ideia de aproximação. Por exemplo, a sequência de números

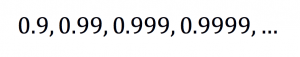
está se aproximando de 1, ou seja, o limite desta sequência é 1. Nem toda sequência possui limite: por exemplo, a sequência

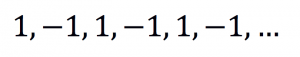
não está se aproximando de um valor fixado a priori, já que infinitos elementos dela são iguais a 1 e também infinitos deles são iguais a -1.

A ideia de limite parece bem intuitiva quando pensamos na sequência

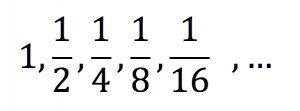
Repare que, a cada passo, nos aproximamos do zero percorrendo metade da distância até ele sem nunca chegar lá.

Apesar de parecer intuitiva, demorou muito tempo para a civilização conseguir lidar com a ideia de limite. O método da exaustão utilizado pelos gregos para calcular áreas e volumes por aproximação (por poliedros) pode ser visto como um de seus precursores. A ideia já estava bem mais amadurecida com o chamado Cálculo Infinitesimal, introduzido por Leibniz e Newton no século XVIII. Os primeiros a formalizar a noção foram os matemáticos Bolzano e Weierstrass — que, no século seguinte, elaborou a definição na forma que usamos agora.

Por que a ideia de limite trouxe tantas mudanças para a Matemática? É por meio desse conceito que podemos compreender claramente os números reais, o infinito e o infinitamente pequeno (infinitésimo). O limite está na base de todos os conceitos importantes do Cálculo. Só depois do aparecimento do Cálculo é que a Matemática desenvolveu as ferramentas para lidar com o movimento. Antes disso, só usávamos Matemática para contar e medir.

A ideia de limite permite inúmeras aplicações da Matemática aos fenômenos físicos. Credit: Jiang Dao Hua, Shutterstock.

Outro exemplo de aplicação prática da Matemática nos fenômenos físicos. Por Boris23 – Obra do próprio, Domínio público, https://commons.wikimedia.org/w/index.php?curid=30983