Gabrielle acaba de ingressar na universidade, mas seu gosto pela Matemática foi despertado ainda na Educação Básica, por meio da OBMEP (Olimpíada Brasileira de Matemática das Escolas Públicas). Teve bons professores de Matemática, mas o que mudou seu olhar foi a pré-Iniciação Científica [oferecida a todos os medalhistas da OBMEP], que fez quando estava nos Ensinos Fundamental e Médio. “Uma vez minha avó estava fazendo tricô e eu falei ‘Vó, você fez um fractal!’, e ela: ‘Que é isso, menina?’. Aí eu fui procurar na Internet para mostrar para ela, e então achei um vídeo explicando sobre crochê e Matemática, e eu me fascinei.” Para ela, é importante tornar a Matemática mais concreta e acessível. “Muitas vezes se esquece que a Matemática é uma linguagem da natureza. Ela é estudada de uma forma que se resume a contas, sem conectar essas contas com o que elas representam, com o objeto de estudo, que é a natureza. O ser humano é apto a encontrar padrões na natureza, e a Matemática é uma linguagem que explica esses padrões.”

Euclides de Alexandria era um matemático grego que viveu cerca de 300 anos AEC e escreveu o que se tornou provavelmente o mais famoso livro de matemática: Elementos. A geometria que aprendemos na escola é apresentada por Euclides nesse livro usando axiomas, princípios que são aceitos como verdadeiros (como um dogma); desses axiomas são deduzidas as propriedades e teoremas. Por exemplo, “existe uma única reta passando por dois pontos dados” é um axioma, enquanto que “a soma dos ângulos internos de todo triângulo é igual a 180˚” é um teorema.

Se pensamos na superfície da terra, não é mais verdade que a soma dos ângulos internos de um triângulo é 180˚. Imagine um triângulo com vértices no Polo Norte, e em dois pontos do Equador, como na figura abaixo.  A soma dos ângulo internos dá 270˚ já que todos os ângulos medem 90˚.

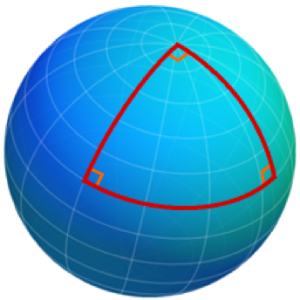
Superfície esférica, como a terrestre.

Esse exemplo mostra que podemos sonhar com outras geometrias, onde nem todos os axiomas de Euclides valem. O húngaro János Bolyai mostrou que poderia criar uma nova geometria (consistente), onde não era válido o quinto axioma de Euclides: “dados uma reta e um ponto fora dela, existe uma única reta que passa pelo ponto e é paralela à reta dada”.

Satisfeito com a descoberta, escreveu para seu pai: “do nada, eu criei um novo e estranho universo”.

De fato esse é também o trabalho de alguns matemáticos: criar novos universos. Talvez algum deles seja até o universo em que vivemos, cuja geometria ainda não conhecemos. Como enxergar esses universos? Essa é uma tarefa que pode beirar o impossível.

Outra geometria interessante pode ser vista no chamado Plano Hiperbólico,  que é difícil de representar concretamente.  Corais marinhos são modelos físicos aproximados. A professora Daina Taimina, da Universidade de Cornell, teve a ideia de fazer modelos de Planos Hiperbólicos em crochê, que permite certas construções elaboradas e mais robustas que as de papel. Essa iniciativa acabou se tornando um grande projeto, com exposições e livros publicados.

As peças de crochê convidam a brincar, ficar mexendo e virando. Isso ajuda a entender um conceito matemático complicado e é bem divertido!

Peça de crochê hiperbólico.

Coral marinho.